Exploring the Impact of Mathematics on Data Science: Recent Trends and Innovations
In the rapidly evolving world of data science, mathematics is the backbone supporting a myriad of advancements and innovations. As data-driven decisions become increasingly crucial across various industries, the role of mathematics has never been more pivotal. This blog explores the recent usage of mathematics in data science, highlighting key trends and innovations that are shaping the future of this dynamic field.
1. Data Visualization and Geometry
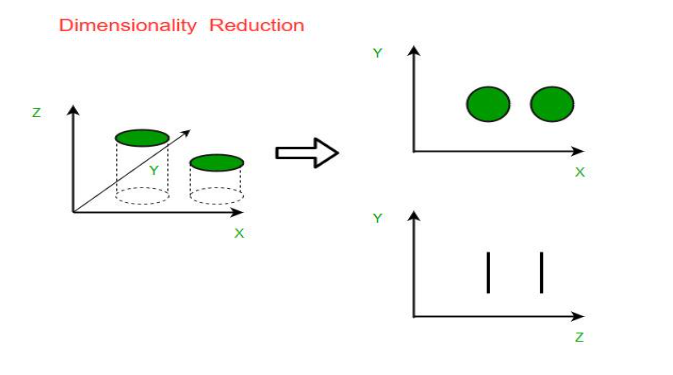
Data visualization is crucial for interpreting complex datasets, and mathematical principles are central to effective visualization techniques. Geometric and topological concepts are used to create visualizations that reveal patterns, trends, and relationships within the data. Tools such as t-SNE (t-distributed Stochastic Neighbor Embedding) and UMAP (Uniform Manifold Approximation and Projection) apply manifold learning to visualize high-dimensional data in lower dimensions.
Example: In exploratory data analysis, dimensionality reduction techniques help visualize clusters and outliers, making it easier to understand the structure of large datasets.
2. Statistical Learning Theory
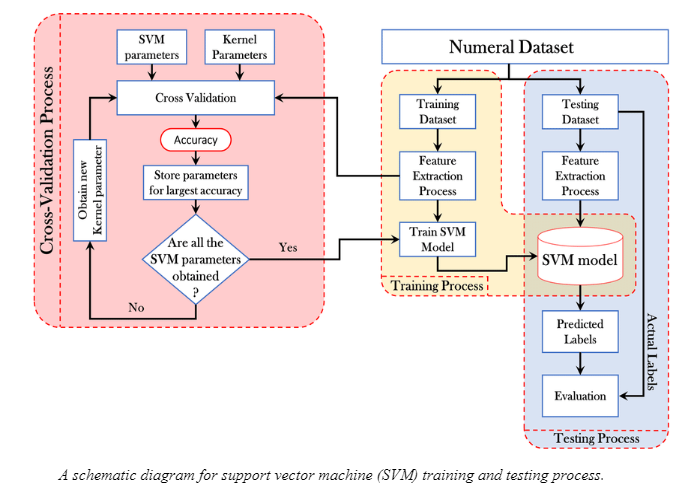
Statistical learning theory provides the theoretical foundation for many machine learning algorithms. Recent advancements in this area focus on understanding the trade-offs between model complexity and generalization. Concepts such as Vapnik-Chervonenkis (VC) dimension and Rademacher complexity are used to analyze the capacity of models and prevent overfitting.
Example: The development of support vector machines (SVMs) and kernel methods has been informed by statistical learning theory, leading to more accurate and robust models for classification tasks.
3. Quantum Computing and Mathematics
Quantum computing represents a frontier in both mathematics and data science. Recent research explores how quantum algorithms can solve complex problems more efficiently than classical counterparts. Quantum mechanics and linear algebra play a significant role in designing quantum algorithms and understanding their potential impact on data science applications.
Example: Quantum algorithms such as Grover’s algorithm and Shor’s algorithm are being studied for their potential to revolutionize optimization and cryptography in data science.
4. Ethics and Fairness
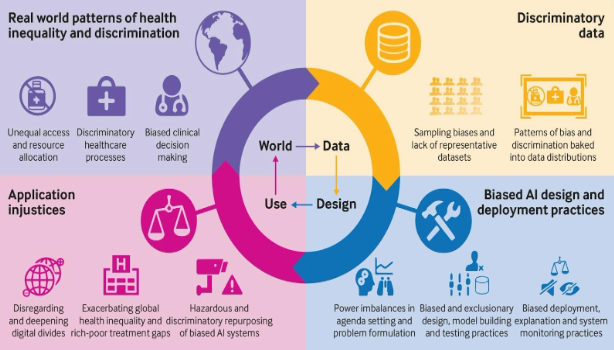
Mathematics also intersects with the ethical considerations in data science. Mathematical techniques are being developed to address issues of fairness, transparency, and bias in algorithms. Methods such as fairness-aware machine learning and algorithmic transparency involve mathematical formulations to ensure equitable outcomes and interpretability.
Example: Techniques for mitigating bias in machine learning models include fairness constraints and reweighting methods that use mathematical optimization to ensure more balanced predictions across different demographic groups.
Conclusion:
Mathematics continues to be a driving force behind the advancements in data science, influencing everything from statistical methods and machine learning algorithms to data visualization and quantum computing. As the field evolves, ongoing mathematical research and innovations will play a crucial role in shaping the future of data science. By leveraging mathematical principles, data scientists can uncover deeper insights, improve model performance, and address complex challenges in an increasingly data-driven world.
Understanding these mathematical foundations not only highlights the significance of mathematics in data science but also underscores the potential for future breakthroughs that will further transform the way we analyze and interpret data.